計算による酵素の熱安定性の予測
田村 康一(研究開発部)
NOVEMBER 2024
はじめに
酵素は多様な化学反応を触媒する生体高分子(主にタンパク質)であり、金属触媒に比べて環境負荷が低く、高い選択性を持つなどの優れた特徴を持つことから、工業・食品などの様々な用途で用いられています。一般に、化学反応速度は温度に依存し、温度が上昇すると反応速度も増加します。これは加温によって反応の活性障壁を乗り越えるためのエネルギーが供与されるためです。例として、無機鉄系触媒を用いて窒素と水素からアンモニアを合成する反応であるハーバー・ボッシュ法では、温度が 500℃ 近くに設定されるようです。一方で、生体高分子である酵素はそのような苛烈な条件に耐えることができず、ある温度でアンフォールド(unfold)し壊れます。この温度を melting temperature (Tm) と呼びます。Tm は、酵素の熱安定性を評価するための重要な指標であり、これを予測しさらに改善することがタンパク質工学における重要な課題となっています。digzyme では、より幅広いニーズに応えるために、酵素の Tm に相関するスコアを計算で予測する手法を開発し、高温で機能する酵素の選抜や、酵素機能の改良に用いています。本ブログでは、実験から得られたタンパク質の熱安定性に関する 2 つのデータセットを用いて、開発した方法の性能を評価します。
方法論
一般に、酵素探索や酵素改変の文脈で熱安定性予測の対象となる酵素は、由来する生物種と所属するタンパク質ファミリーが多岐にわたるので、予測モデルにはこれら2つの要素に依存しない汎用性が求められます。この要請を満たすためにこれまで様々な方法が提案されてきており、それらは次の 2 つに大別されます。
1.データ駆動型アプローチ
2.物理ベースモデルによるアプローチ
1.は、主に機械学習と呼ばれるアプローチで、実験によって得られた大量のデータから、タンパク質の熱安定性を予測するための法則(モデル)を構築します。このモデル構築過程を訓練と呼びます。訓練に要する時間は、データの量やモデルの複雑さに依存し、コーヒー1杯を飲んでる間に終わることもあれば、最新の GPGPU (計算を加速するための装置)を用いて1週間丸々かける場合もあります。いったん訓練済みモデルを構築すれば、その後の予測のステップの計算コストは訓練過程に比べて低いです。
そのモデル構築の方法から推察されるように、機械学習モデルの精度は学習データの量と質に大きく依存します。学習データが少ないと、見出される法則性にバイアスがかかることは明らかです。また、学習データが特定の生物種やタンパク質ファミリーに偏っていないか注意する必要もあります。さらに、タンパク質の物性値を測定するときの実験条件も揃っていることが望ましいですが、これは様々な研究グループからの実験データがデータベースに蓄積される現状を考慮すると、実現は困難であると言えるでしょう。
学習データの量と偏りに注意したとしても、依然として汎用性に問題が残る場合があります。それが過学習と外挿性の問題です。過学習とは、機械学習モデルが学習データに過剰に適合している状態を指します。この状態のモデルは、訓練に使用したデータに対しては非常に優れた予測精度を与えますが、それ以外のデータに対しては全く無力です。過学習を防ぐには、モデルの複雑さを適切に制御するなどの専門的な技術が必要となります。外挿性とは、学習データがカバーする領域外のデータに対する有効性のことです。タンパク質の文脈でいえば、学習データに似ていない(相同性が低い)新規なアミノ酸配列に対しても予測の信頼性を担保できる能力を指します。これは、酵素探索や改変においてクリティカルな問題になります。というのも、大抵の場合、物性値を予測したい新規酵素の既知配列(論文に物性値が報告されているようなアミノ酸配列)に対する相同性は低いからです。このように重要な能力である外挿性ですが、単純な線形モデル以外では、それを内在的に組み込んだモデルを構築することは困難です。従って、ここでのベストプラクティスは、「構築した機械学習モデルの適用範囲をよく理解して使うこと」となります。
2.の物理ベースモデルでは、原子間相互作用を記述するエネルギー関数の構築が予測モデル構成の出発点になります。原子・分子のような極微の世界を支配する普遍的な自然法則の数学的表現(方程式)は 100 年程度前からすでに知られており、最も簡単な例でその方程式を手で解き、実験値と比較することで、その予測の精確さを実感することができます(気になる人は、大学初年級の物理化学の教科書を参照してください)。この方程式は(光速やプランク定数などの)物理定数以外の人為的なパラメータを一切含まないので、適用範囲に普遍性があります。しかし、我々が興味を持つような多原子系(=酵素+溶媒)ではこの方程式は非常に複雑になり、最先端の計算機を用いても現実的な時間内に計算が終わることはないでしょう。そのため、実際には様々な近似を導入し、精確さと普遍性を代償にすることで方程式を簡単化し計算が可能な範囲に落とし込みます。この近似手法が、構築した物理モデルの精確さと適用可能範囲を定義することになります。近似手法として頻繁に用いられるものとしては、
●分子力学ベースの経験的エネルギー関数の導入
●統計力学理論による溶媒の取り扱い
があります。前者では、簡単な関数形を仮定し、人為的なパラメータセットを導入することで、本来複雑な原子間相互作用を(かなり)簡単に記述します。後者では、酵素の周囲に存在する多数の溶媒分子を明示的に表現することはやめて、ある種の平均的な量で置き換えてしまいます。これらの大胆な近似は計算コストを大幅に削減してくれますが、先に述べたようにその精確さと普遍性は損なわれています。
digzyme score
digzymeでは、酵素の熱安定性を予測するために、物理ベースモデルを採用しています。このモデルでは、酵素の立体構造情報を入力すると、あるスコア(とりあえず ”digzyme score” と呼びます)を出力します。このスコアは酵素の Tm と相関があるように設計されており、通常 1.0 付近の値をとります。回帰モデルではないので、 Tm そのものの値を予測するわけではありませんが、普通は複数酵素間の安定性の差だけを知れれば十分なので、このような仕様になっています。
事例 1. 変異体の熱安定性の予測
酵素の有用変異体を計算で設計し選抜するためには、多数の候補変異体の各種プロパティを計算し、それらの値に基づいて変異体をランク付けする必要があります。プロパティの中でも重要視されるのが熱安定性です。以下では、変異体の熱安定性予測のコンテストにおける複数グループと digzyme の結果を比較します。
鉄-硫黄クラスターの再生に関わる酵素である frataxin の 8 つの変異体について、野生型と変異体のアンフォールディング自由エネルギーの差(ΔΔGu)を計算で予測するコンテストが 2018 年に実施され[1]、その結果が 2019 年に論文として出版されました[2]。アンフォールディング自由エネルギー(ΔGu)は、式 (1) で示される、
ΔGu = Gu - Gf (1)
酵素のアンフォールディングに付随する自由エネルギー変化と定義されます。ここで Gu, Gf はそれぞれアンフォールド状態とフォールド状態の自由エネルギーです。一般に、酵素はフォールド状態の方が安定なので、ΔGu > 0 となります。ΔGu が大きいほど、酵素はアンフォールドし難い(=安定である)ことに注意してください。野生型と変異体のそれぞれについて、式(1) で定義されるアンフォールディング自由エネルギーを測定し、その差をとることで、変異によるアンフォールディング自由エネルギーの変化が以下のように計算できます:
ΔΔGu = ΔGu(変異体) - ΔGu(野生型) (2)
ΔΔGu < 0 ならば、変異によって酵素が不安定化したことになります。
Figure 1左に、 digzyme が計算した予測スコア(”digzyme score”)と実験値を示します。ピアソン相関係数は 0.87 でした。 これは既存の物理ベースの手法として popular な FoldX よりも僅かに良い結果です(Figure 1右)。
他の物理ベースの手法としては、 Pal Lab のグループが分子動力学法(molecular dynamics, MD)ベースの方法による予測を行っています。この方法では、 MD による構造サンプリング(1 ns)を行い、サンプリングされた構造を folded state と unfolded state にクラスタリングしています。その後、それぞれのクラスターの代表構造に対してエネルギー計算を行い、式(1)の値が算出されます。この計算を野生型と変異体について実行することで、式(2)から実験値との比較が可能な値を得ることができます。しかし、MD 開始構造である folded state のタンパク質が、この計算条件(27℃、通常の平衡 MD)にて 1 ns 以内に unfolded state に構造遷移するという前提には明らかに無理があります。というのも、fast-folding protein と呼ばれる、比較的短時間でフォールド/アンフォールドするタンパク質の Tm 付近でのシミュレーションにおいてさえ、構造遷移が生じるのにこの 1000 倍以上の時間がかかるからです[3]。したがって、この方法でも中程度の相関が存在した(Figure 1右)のは、偶然の結果と言っても過言ではないでしょう。
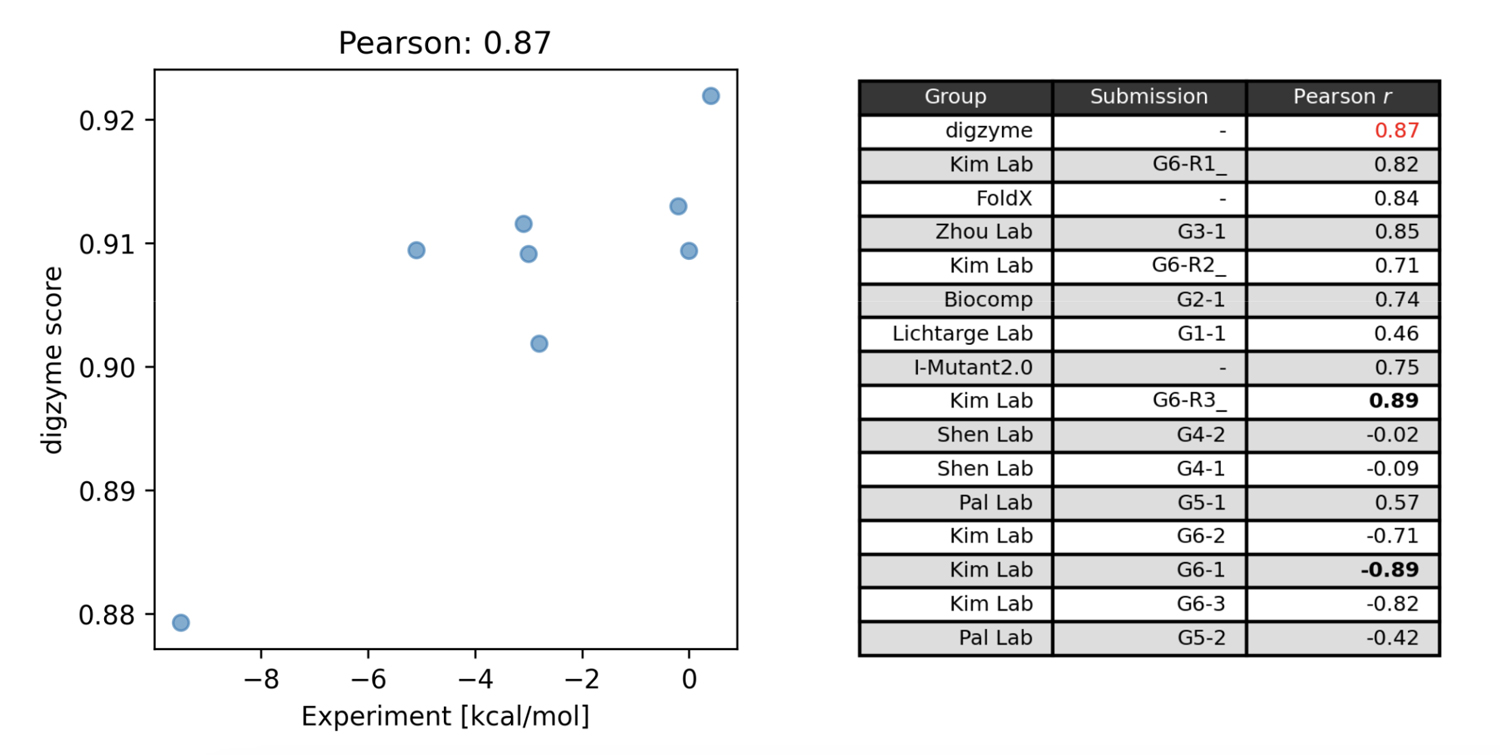
コンテストで最も相関の大きいモデルを提案したのは Kim Lab のグループで、相関係数の絶対値は 0.89 でした(Figure 1右)。このグループは機械学習モデルでの予測を行っており、Protherm データベースに登録されている変異体の熱安定性のデータを学習に利用しています[4]。この機械学習モデルでは、構造ベースとアミノ酸配列ベースの特徴量がそれぞれ計算され、これらの特徴量を用いて勾配ブースティング木によって回帰モデルが構築されます。構造ベースの特徴量の中には物理モデルである FoldX の計算値が含まれており、この値が最も重要な特徴量であることが知られています[4]。この事実は、FoldX の予測と同程度の精度を有する物理モデルの digzyme score を使用することで、さらに高度な機械学習モデルを構築できる可能性を示唆しています。目的の酵素について、大量の変異体データが存在する場合は、専用のモデルの構築を試みても良いかもしれません。
事例 2. 同一機能酵素の熱安定性の予測
有用酵素の酵素探索では、同一機能(と予測される)酵素のアミノ酸配列をデータベースから多数抽出し(母集団の形成)、それらを何らかの指標でランキングすることで候補酵素を選定します。変異体設計と同様に、このときも熱安定性が重要な指標の1つになります。
ここでの熱安定性の予測は、事例 1.でみたような野生型と変異体の差の予測とは趣が異なることに注意してください。通常、野生型と変異体ではアミノ酸配列の長さは同じであり、配列一致度は 99% に近いことが多いです。これに対し、特定の機能に絞ってデータベースから抽出した配列の母集団では、アミノ酸配列の長さはまちまちであり、互いの一致度は低いことが一般的です。このような集団に対して熱安定性を予測し配列のランキングを作成することは、以下に示すように困難である場合が多いです。
ここでの事例は、2024 年の 9 月にプレプリントサーバーに投稿された、ナノボディ(抗体の小断片)の Tm の大規模なデータセット NanoMelt です[5]。これは既存のデータに、著者らが独自に測定したデータを追加したデータベース(640 データ)で、タンパク質の濃度、pH やバッファーなどの実験条件が揃えられています。このデータセットに対し、事例 1.と同じ物理モデルで各酵素に対して digyzme score を計算し、実験値との相関を確認します。
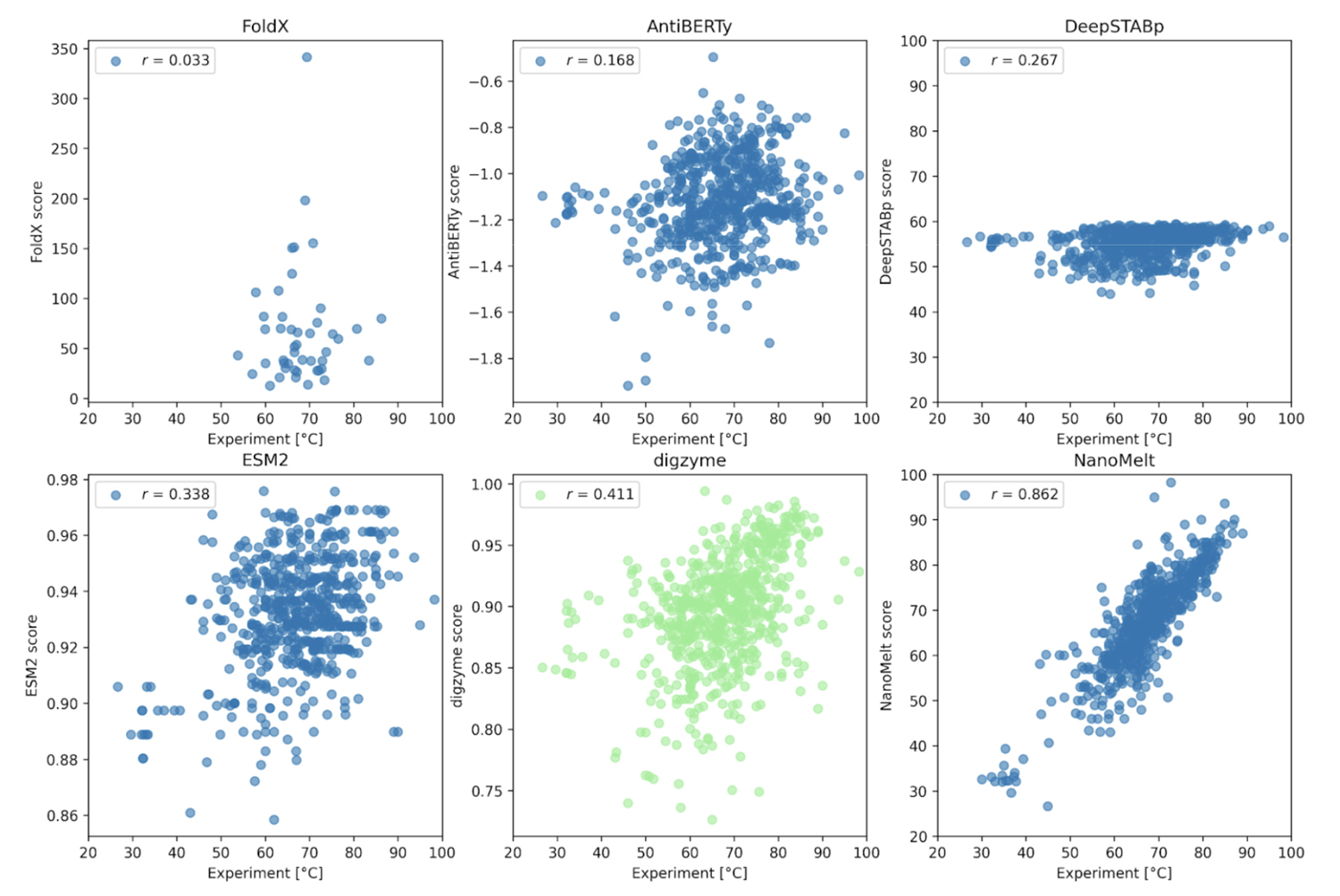
Figure 2. に示すように、 NanoMelt データセットそのものを学習対象とした結果(Figure 2下段右)以外は、実験値と予測結果の相関は存在しないか低いです。まず、事例 1.では高い相関係数を達成した物理モデルである FoldX は、ここでは相関のある予測結果を出力することはできませんでした。これに対し、digzyme では弱いながらも相関のある結果を予測することに成功しました(r = 0.411, Figure 2下段中央)。データを FoldX の予測に使用した 46 個のアミノ酸配列に限定した場合でも弱い相関が存在した(r = 0.273)ことから、これは既存の物理モデルからの適用可能範囲の拡大という意味において顕著な進歩であると言えます。AntiBERTy と ESM-2 はタンパク質の言語モデルであり、Figure 2 のスコアの実態は、アミノ酸配列の (pseudo) log-likelihood です[5]。これは配列の確らしさの指標であり、熱安定性とのある程度の相関が期待されましたが、実際には弱い相関があるのみでした(相関係数はそれぞれ 0.168 と 0.338)。従って、著者らが示すように、これらの言語モデルを使って熱安定性予測を行うとしたら、更なる学習によって専用タスクに特化したモデルを構築した方がよいでしょう[5]。一方で、Tm を予測するための専用回帰モデルである DeepSTABp の相関の低さ(r = 0.267, Figure 2上段右)についてはよく考慮する必要があります。元の論文[6]によると、DeepSTABp のテストデータに対するピアソン相関係数は 0.90 と、顕著な結果を出しています。それにも関わらず、NanoMelt データセットに対する相関係数が低かったことは、このモデルが過学習に陥っており、汎化能力に限界がある(「馴染みのないデータ」に対して無力である)ことを示唆しています。これに対し、digzyme が採用している物理モデルは物理法則という一般的な原理がモデル構築の基礎であるため、適用できるアミノ酸配列の範囲に基本的に限界はありません。実際に、DeepSTABp よりも高い相関を与えていることからも、物理モデルの優位性がある程度示されたと言えるでしょう。
さて、強い相関(r = 0.862, Figure 2下段右)を示している NanoMelt のモデルですが、過学習の有無が気になるところです。残念ながら、NanoMelt はナノボディ専用モデルであるため、任意のタンパク質配列を含む他のデータセットでその性能を再評価することは困難です。そのため、著者らはラクダのナノボディ配列のデータベースから配列を新たに 6 つ選定し、実験で Tm を測定することでモデルの再評価を行っています。配列の選定基準は以下の 3 つです:
1.NanoMelt データセットの中の最も類似している配列との不一致度が、少なくとも 30% である
2.AbNatiV VHH-nativeness スコア(配列の確からしさの指標)が 0.85 以上である
3.NanoMelt で予測した Tm が低い(Tm < 61 ℃)、もしくは高い(Tm > 73 ℃)
これらの 6 配列のうち、 Tm が低いと予測された 3 配列は発現しませんでしたが、一方で、Tm が高いと予測された 3 配列は発現し、 Tm の測定に成功しました。その予測結果との誤差は 1 ℃ 程度であり、NanoMelt の高い予測性能が示されました[5]。この結果を以って過学習の有無を断ずることはできませんが、NanoMelt モデルの適用可能範囲を把握するための手がかりにはなるでしょう。
終わりに
酵素探索や改変の文脈では、酵素の熱安定性を計算で評価し精確なランキングを作成することが、後の実験の工程を減らすために重要となります。digzyme では、汎用的な物理モデルを適用することで、この課題に挑戦しています。本ブログでは、2 つのデータセットに対する予測スコアの計算によって、開発したモデルの評価を行いました。事例 1. に示すように、変異体の熱安定性予測では実用レベルの精度を持つことが明らかになりました。一方で、任意のアミノ酸配列間の比較に関しては、事例 2. に示すように、既存の物理モデルや機械学習モデルに対する優位性が示されたものの、実験値との相関は弱く、未だ改善の余地があることもわかりました。
昨今では、 AI による酵素設計の成功例が増えてきており、生命進化の過程で取りこぼされた新規なフォールド(構造)および機能の実現が期待されていますが、その新規性が機械学習による(熱安定性などの)物性予測を困難たらしめることは想像に難くありません。そのため、本ブログで紹介したような、学習データに依存しない汎用的な物理モデルの重要性がますます高まると考えられます。digzyme では、より精確で信頼性の高いモデルを構築するために、今後も積極的に研究開発を進めていく予定です。
参考文献
[1] CAGI5 Frataxin [Link]
[2] Savojardo et al. Hum. Mutat., 2019, 40(9), 1392 [Link]
[3] Lindorff-Larsen et al. Science, 2011, 334, 517 [Link]
[4] Berliner et al. PLoS ONE, 2014, 9(9), e107353 [Link]
[5] Ramon et al. bioRxiv, 2024 [Link]
[6] Jung et al. Int. J. Mol. Sci., 2023, 24(8), 7444 [Link]
